Graphs
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of nodes. Throughout these problems we will represent nodes with single characters.
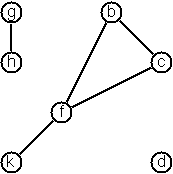
There are several ways to represent graphs. One method is to represent each edge separately.
Edge-clause form
type alias Edge comparable = (comparable, comparable)
edges80 = [ ('b','c'), ('b','f'), ('c','f'), ('f','k'), ('g','h')]
We call this edge-clause form. The edge-clause cannot represent isolated nodes.
Graph-term form
To represent the whole graph we can use as a pair of sets (nodes and edges).
type alias Graph comparable = (List comparable, List (Edge comparable))
graph80 = ( [ 'b', 'c', 'd', 'f', 'g', 'h', 'k' ],
[ ('b','c'), ('b','f'), ('c','f'), ('f','k'), ('g','h') ] )
We call this the graph-term form. It will be our default representation in these problems. Note that the lists should be kept sorted and should not include duplicated elements. Each edge appears only once in the edge list; i.e. an edge ('x','y') represents one edge between x and y. The term ('y','x') is not shown.
| Elm Leaf |
|---|
Because these forms require nodes and edges to be sorted and/or have duplicated remove the nodes must be of type comparable. This limits us to number, Char, String, lists of comparables or tuples of comparables. |
Adjancency list form
A third representation method is to associate with each node the set of nodes that are adjacent to that node. We call this the adjacency-list form. In our example:
type alias AdjList comparable = List((comparable, List comparable))
adjList80 =
[ ('b',['c','f']),
('c',['b','f']),
('d',[]),
('f',['b','c','k']),
('k',['f']),
('h',['g'])
]
Human-readable form
Typing the terms by hand is cumbersome and error-prone. We can define a more compact and "human-readable" notation as follows:
hm80 = "[b-c, f-c, g-h, d, f-b, k-f, h-g]"
We call this the human-friendly form. The list does not have to be sorted and may even contain the same edge multiple times. Notice the isolated node d. Unlike the Graph and AdjList type, this is textual representation, not a type.
Directed Graphs
When the edges are directed we call them arcs. These are represented by ordered pairs. Such a graph is called directed graph. We can reuse the graph notation with little or no change, to represent digraphs.
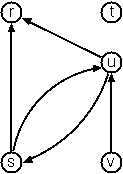
type alias Arc comparable = (comparable, comparable)
arcs80 = [ ('s','r')
, ('s','u')
, ('u','r')
, ('u','s')
, ('v','u')]
type Digraph comparable = (List comparable, List (Arc comparable))
type DirAdjList comparable = List((comparable, List comparable))
digraph80 = ( [ 'r', 's', 't', 'u', 'v'], arcs80 )
dirAdjList80 = [ (r,[])
, (s,[r,u])
, (t,[])
, (u,[r])
, (v,[u])
]
-- human-readable digraph
hrDigraph80 = "[s > r, t, u > r, s > u, u > s, v > u]"
Labeled graphs
Finally, graphs and digraphs may have additional information attached to nodes and edges (arcs). For edges and arc we have to extend our notation. Graphs with additional information attached to edges are called labeled graphs.
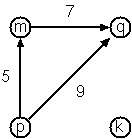
type alias Arc comparable = (comparable, comparable, Int)
labeledArcs80 =
[ ('m', 'q', 7)
, ('p', 'q', 9)
, ('p', 'm', 5)
]
lDigraph80(['k', 'm', 'p', 'q'], labeledArcs80)
type alias LabeledDirAdjList comparable = List((comparable, List (comparable, Int)))
lDirAdjList80 = [ ('k', [])
, ('m', [ ('q',7) ])
, ('p', [ ('m',5), ('q',9) ])
, ('q', [])
]
lhr80 = "[p>q/9, m>q/7, k, p>m/5]"
Problems
Problem 80a - Convert from a graph from graph-term to adjacency-list representation.
Problem 80b - Convert from a graph from adjacency-list to graph-term representation.
Problem 81 - Find the path between two nodes.
Problem 83 - Generate all spanning trees of a graph.
Problem 84 - Construct the minimum spanning tree of a graph.
Problem 85 - Determine if two graphs are isomorphic.
Problem 86a - Determine the degree of all nodes of a graph.
Problem 86b - Use the Welch-Powell algorithm to color the nodes of a graph such that adjacent nodes have different colors.
Problem 87a - Extract the nodes of a graph in depth-first order.
Problem 87b - Extract the nodes of a graph in breadth-first order.
Problem 88 - Split a graph into its connected components.