Problem 64

To draw a tree a layout algorithm determines the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is illustrated below:

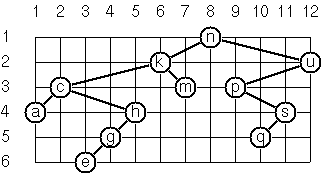
In this layout strategy, the following two rules determine the position:

• x(v) is equal to the position of the node v in the inorder sequence
• y(v) is equal to the depth of the node v in the tree.

Write a function to annotate each node of the tree with its position. To solve this problem you will need to traverse the tree. Problems 68a, 68b, and 68c examine tree traversal.

Example

tree64 = 
  Node 'n'
    (Node 'k'
      (Node 'c'
        (Node 'a' Empty Empty)
        (Node 'h'
          (Node 'g'
            (Node 'e' Empty Empty)
            Empty)
          Empty))
      (Node 'm' Empty Empty))
    (Node 'u'
      (Node 'p'
        Empty
          (Node 's'
            (Node 'q' Empty Empty)
            Empty))
      Empty)

layout tree64 ==  
  Node ('n',(8,1)) (Node ('k',(6,2)) (Node ('c',(2,3)) ...

Unit Test

import Html
import List


type Tree a
    = Empty
    | Node a (Tree a) (Tree a)


tree64 = 
  Node 'n'
    (Node 'k'
      (Node 'c'
        (Node 'a' Empty Empty)
        (Node 'h'
          (Node 'g'
            (Node 'e' Empty Empty)
            Empty)
          Empty))
      (Node 'm' Empty Empty))
    (Node 'u'
      (Node 'p'
        Empty
          (Node 's'
            (Node 'q' Empty Empty)
            Empty))
      Empty)


layout : Tree a -> Tree (a, (Int, Int))
layout tree =
    -- your implementation here
    Empty


main =
    Html.text
        (if (test) then
            "Your implementation passed all tests."
         else
            "Your implementation failed at least one test."
        )


test : Bool
test =
    let 
        t = layout tree64 
    in 
        List.all ((==) True)
          [ t == layout64
          ]

layout64 = 
  Node ('n', (8, 1))
    (Node ('k', (6, 2))
      (Node ('c', (2, 3))
        (Node ('a', (1, 4)) Empty Empty)
        (Node ('h', (5, 4))
          (Node ('g', (4, 5))
            (Node ('e', (3, 6)) Empty Empty)
            Empty)
          Empty))
      (Node ('m', (7, 3)) Empty Empty))
    (Node ('u', (12, 2))
      (Node ('p', (9, 3))
        Empty
        (Node ('s', (11, 4))
          (Node ('q', (10, 5)) Empty Empty)
          Empty))
      Empty)

Hints

1. You can simplify the problem by breaking down into two or more steps, traversing once to set the X, once to set the Y. You can model List.indexedMap to create traversal functions wtih depth or in-order.
2. The problem can be solved in a single traversal. You'll probably need nested let clauses to get the in-order values from subtree traversals.

Solutions

Solutions